For single-cell data, cell-level network analysis can be performed based on joint similarity in alpha chain sequence and beta chain sequence.
We simulate some toy data to demonstrate the usage.
set.seed(42)
library(NAIR)
dat <- simulateToyData(chains = 2)
head(dat)
#> AlphaSeq BetaSeq Count UMIs SampleID
#> 1 TTGAGGAAATTCG TTGAGGAAATTCGG 3095 4 Sample1
#> 2 GGAGATGAATCGG GGAGATGAATCGG 3057 6 Sample1
#> 3 GTCGGGTAATTGG GTCGGGTAATTGGG 3575 8 Sample1
#> 4 GCCGGGTAATTCG GCCGGGTAATTCGG 3994 7 Sample1
#> 5 GAAAGAGAATTCG GAAAGAGAATTCGG 3670 3 Sample1
#> 6 AGGTGGGAATTCG AGGTGGGAATTCG 4076 5 Sample1The input data is assumed to have the following format:
- Each row corresponds to a unique cell
- The data contains separate columns for alpha chain sequence and beta chain sequence
Dual-chain network analysis can be performed using
buildRepSeqNetwork() (or
generateNetworkObjects()) by supplying a length-2 vector to
the seq_col parameter:
- First entry should reference the column for alpha chain sequence
- Second entry should reference the column for beta chain sequence
# Build network based on joint dual-chain similarity
network <- buildNet(dat,
seq_col = c("AlphaSeq", "BetaSeq"),
count_col = "UMIs",
node_stats = TRUE,
stats_to_include = "all",
cluster_stats = TRUE,
color_nodes_by = "SampleID",
size_nodes_by = "UMIs",
node_size_limits = c(0.5, 3)
)We print the network graph plot with labels added for the largest two clusters:
addClusterLabels(network$plots$SampleID, network, top_n_clusters = 2, size = 8)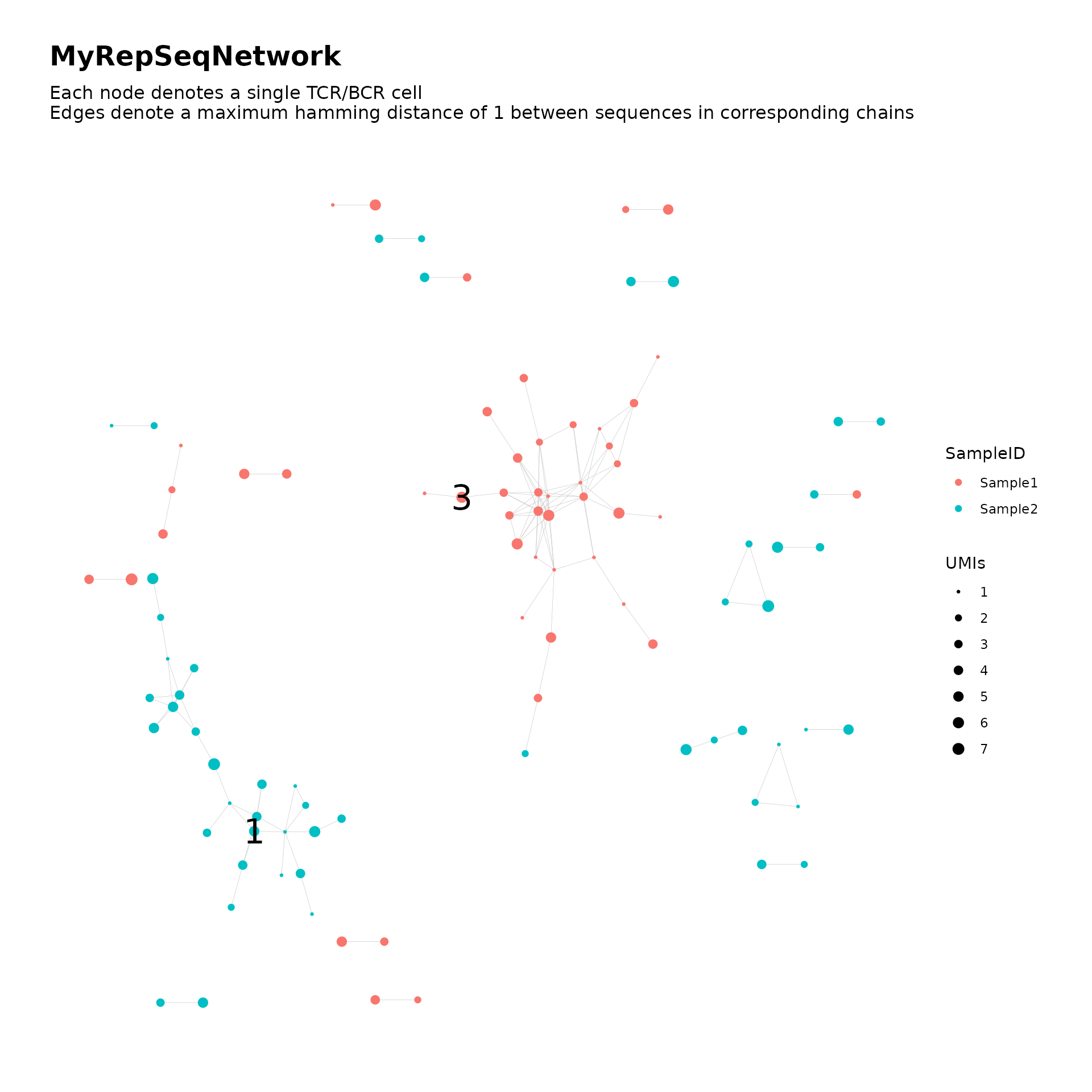
The list returned buildRepSeqNetwork() the following
items:
names(network)
#> [1] "details" "igraph" "adjacency_matrix" "adj_mat_a"
#> [5] "adj_mat_b" "node_data" "cluster_data" "plots"Notice that the list contains three adjacency matrices:
adjacency_matrix corresponds to the network based on joint
similarity in both chain sequences, while adj_mat_a
corresponds to the network based only on similarity in the alpha-chain
sequence (and similarly for adj_mat_b).
The cluster-level data contains sequence-based cluster statistics for each of the alpha and beta chain sequences:
head(network$cluster_data)
#> cluster_id node_count eigen_centrality_eigenvalue eigen_centrality_index
#> 1 1 15 3.680389 6.385488e-01
#> 2 2 13 4.419380 6.131393e-01
#> 3 3 16 7.257172 5.291669e-01
#> 4 4 10 3.750958 6.107669e-01
#> 5 5 3 1.414214 5.857864e-01
#> 6 6 3 2.000000 8.881784e-16
#> closeness_centrality_index degree_centrality_index edge_density
#> 1 0.4497821 0.3190476 0.1809524
#> 2 0.4357891 0.3141026 0.2692308
#> 3 0.4650078 0.3250000 0.3416667
#> 4 0.4889192 0.3555556 0.3111111
#> 5 1.0000000 0.3333333 0.6666667
#> 6 0.0000000 0.0000000 1.0000000
#> global_transitivity assortativity diameter_length max_degree mean_degree
#> 1 0.2884615 -0.16503588 6 7 2.60
#> 2 0.3802817 -0.15180055 7 11 4.00
#> 3 0.6328125 -0.08424855 6 12 5.81
#> 4 0.3750000 -0.33425414 6 6 2.90
#> 5 0.0000000 -1.00000000 3 2 1.67
#> 6 1.0000000 NaN 2 2 2.00
#> mean_A_seq_length mean_B_seq_length A_seq_w_max_degree B_seq_w_max_degree
#> 1 12.13 12.87 AAAAAAAAATTC AAAAAAAAATTCG
#> 2 13.00 13.08 GGGGGGGAATTGG GGGGGGGAATTGG
#> 3 13.00 13.94 GGGGGGGAATTGG GGGGGGGAATTGGG
#> 4 12.00 12.00 AAAAAGAAATTG AAAAAGAAATTG
#> 5 13.00 14.00 AGGGGAGAATTGG AGGGGAGAATTGGG
#> 6 13.00 14.00 AAAAAAGAATTGC AAAAAAGAATTGCG
#> max_count agg_count A_seq_w_max_count B_seq_w_max_count
#> 1 6 42 AAAAAAAAATTC AAAAAAAAATTC
#> 2 6 28 GGGGTGGAATTGG GGGGTGGAATTGG
#> 3 6 49 GGGGAGAAATTGG GGGGAGAAATTGGG
#> 4 7 39 AAAGAAAAATTG AAAGAAAAATTG
#> 5 5 10 AGGGGAGAATTGG AGGGGAGAATTGGG
#> 6 2 4 AGAAAAGAATTGC AGAAAAGAATTGCGThe remainder of the output and customization follows the general case for
buildRepSeqNetwork().